Ejercicio 2: Aletas cuadradas

Enunciado

Encuentre la eficiencia de la siguiente aleta de acero (\(k = 53~\text{W/m}\cdot\text{K}\)), si su largo es \(L = 100~\text{mm}\) y su ancho es igual a su grosor \(t=10~\text{mm}\). Considere que el coeficiente de convección será \(h = 60~\text{W/m}^2\cdot\text{K}\), si la temperatura del seno del fluido es \(20~^\circ\text{C}\) y la temperatura de la pared es \(95~^\circ\text{C}\).

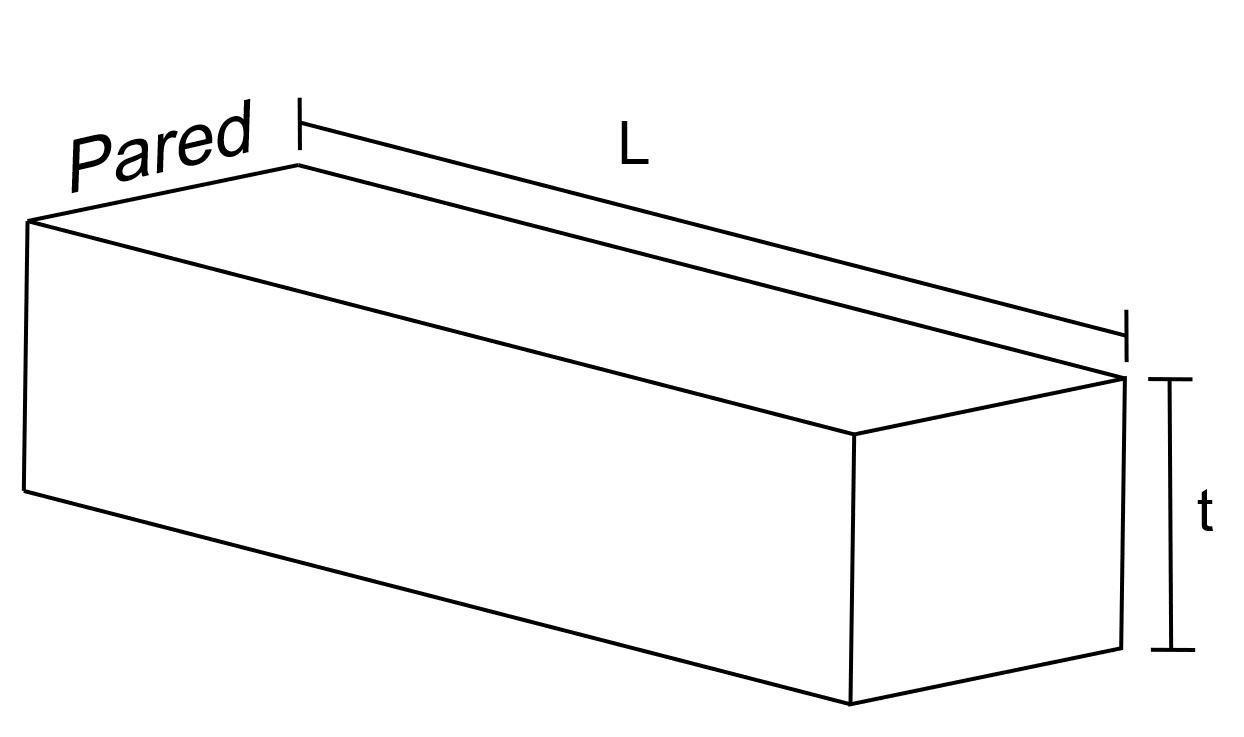
Fig. 12 Aleta cuadrada

Utilizando el mismo volumen de material, usted decide disminuir su grosor a favor de aumentar su ancho. Considere que el mínimo de grosor posible es de \(3~\text{mm}\) y el largo debe mantenerse constante. ¿Cuánto cambia la eficiencia de esta aleta?¿Qué haría usted si solo quisiera aumentar la transferencia de calor?

Ver solución

Solución

from numpy import cosh, sqrt, tanh
import handcalcs.render

Inciso 1 - Cálculo de eficiencia aleta cuadrada

La eficiencia de una aleta vendrá por la comparación entre la capacidad real de una aleta de transferir calor, versus la capacidad máxima de calor transferido.

\[ \eta_f = \frac{q_f}{q_{max}} \]

Sabemos que para la aleta completa, el calor \(q_f\) vendrá dado por:

\[ q_f = \sqrt{hPkA_c}\theta_b\tanh{mL} \]

Donde \(m\) será:

\[ m = \sqrt{\frac{hP}{kA_c}} \]

Ya que la tasa a la cual se transfriere el calor por conducción debe ser equivalente a la tasa de trasnferencia de calor por convección, es posible escribir la misma ecuación de la siguiente manera:

\[ q_f = \int_{A_f} h\theta(x)dA_s \]

Luego, la condición máxima de transferencia de calor implica que la aleta completa se encuente a la temperatura de la base:

\[ q_{max} = hA_f\theta_b \]

Luego despejamos para la eficiencia.

\[ \eta_f = \frac{\sqrt{hPkA_c}\tanh{mL}}{ hA_f} \]

Para una aleta cuadrada, el perímetro y el área transversal de flujo de calor por conduccción serán:

\[ P = 2t + 2w \hspace{2cm} A_c = w\cdot t \]

Mientras que el área de la aleta (\(A_f\)) será todo el área superficial de la aleta.

\[ A_f = P\cdot L + w\cdot t \]

Sin embargo, la convección en la punta de la aleta será 0, ya que trabajamos a partir del supuesto de punta adiabática. Por lo que el área real de superficie de una aleta para la transferencia de calor por convección será \(A_f = P\cdot L\).

Reordenando la ecuación para la eficiencia.

\[ \eta_f = \frac{\sqrt{hP}}{hP}\frac{\sqrt{kA_c}\tanh{mL}}{L} = \frac{1}{\sqrt{hP}}\frac{\sqrt{kA_c}\tanh{mL}}{L} = \frac{\tanh{mL}}{mL} \]

%%render params
k = 53 #W/m$\cdot$K
h = 60 #W/m$^2\cdot$K
L = 100/1000 #m
t = 10/1000 #m
w = t #m
T_inf = 20 #$^\circ$C
T_b = 95 #$^\circ$C

\[\begin{split} \begin{aligned} k &= 53 \; \;\textrm{(W/m$\cdot$K)} &h &= 60 \; \;\textrm{(W/m$^2\cdot$K)} &L &= 0.100 \; \;\textrm{(m)} \\[10pt] t &= 0.010 \; \;\textrm{(m)} &w &= 0.010 \; \;\textrm{(m)} &T_{inf} &= 20 \; \;\textrm{($^\circ$C)} \\[10pt] T_{b} &= 95 \; \;\textrm{($^\circ$C)} \end{aligned} \end{split}\]

%%render long
P = 2*t+2*w #m
A_c = t*w #m$^2$
m = sqrt((h*P)/(k*A_c)) #m$^{-1}$
eta_f = tanh(m*L)/(m*L)

\[\begin{split} \begin{aligned} P &= 2 \cdot t + 2 \cdot w \\&= 2 \cdot 0.010 + 2 \cdot 0.010 \\&= 0.040 \; \;\textrm{(m)}\\[10pt] \\[10pt] A_{c} &= t \cdot w \\&= 0.010 \cdot 0.010 \\&= 0.000 \; \;\textrm{(m$^2$)}\\[10pt] \\[10pt] m &= \sqrt { \frac{ h \cdot P }{ k \cdot A_{c} } } \\&= \sqrt { \frac{ 60 \cdot 0.040 }{ 53 \cdot 0.000 } } \\&= 21.280 \; \;\textrm{(m$^{-1}$)}\\[10pt] \\[10pt] \eta_{f} &= \frac{ \tanh \left( m \cdot L \right) }{ m \cdot L } \\&= \frac{ \tanh \left( 21.280 \cdot 0.100 \right) }{ 21.280 \cdot 0.100 } \\&= 0.457 \\[10pt] \end{aligned} \end{split}\]

Inciso 2 - Cálculo de eficiencia aleta rectangular

El volumen disponible vendrá dado por:

%%render long sci_not
V = w*t*L #m$^3$

\[\begin{split} \begin{aligned} V &= w \cdot t \cdot L \\&= 1.000 \times 10 ^ {-2} \cdot 1.000 \times 10 ^ {-2} \cdot 1.000 \times 10 ^ {-1} \\&= 1.000 \times 10 ^ {-5} \; \;\textrm{(m$^3$)}\\[10pt] \end{aligned} \end{split}\]

Luego el nuevo ancho de la aleta será:

%%render params sci_not
t = 3/1000 #m
w = V/(t*L) #m

\[ \begin{aligned} t &= 3.000 \times 10 ^ {-3} \; \;\textrm{(m)} &w &= 3.333 \times 10 ^ {-2} \; \;\textrm{(m)} \end{aligned} \]

Ya que \(w>>t\) es válido que el perímetro sea escrito de la siguiente manera.

\[ P = 2w \]

Y observamos que el perímetro se mantiene constante para ambas aletas.

%%render params
P = 2*w
A_c = w*t

\[ \begin{aligned} P &= 0.067 \; &A_{c} &= 0.000 \; \end{aligned} \]

%%render long
P = 2*t+2*w #m
A_c = t*w #m$^2$
m = sqrt((h*P)/(k*A_c)) #m$^{-1}$
eta_f = tanh(m*L)/(m*L)

\[\begin{split} \begin{aligned} P &= 2 \cdot t + 2 \cdot w \\&= 2 \cdot 0.003 + 2 \cdot 0.033 \\&= 0.073 \; \;\textrm{(m)}\\[10pt] \\[10pt] A_{c} &= t \cdot w \\&= 0.003 \cdot 0.033 \\&= 0.000 \; \;\textrm{(m$^2$)}\\[10pt] \\[10pt] m &= \sqrt { \frac{ h \cdot P }{ k \cdot A_{c} } } \\&= \sqrt { \frac{ 60 \cdot 0.073 }{ 53 \cdot 0.000 } } \\&= 28.682 \; \;\textrm{(m$^{-1}$)}\\[10pt] \\[10pt] \eta_{f} &= \frac{ \tanh \left( m \cdot L \right) }{ m \cdot L } \\&= \frac{ \tanh \left( 28.682 \cdot 0.100 \right) }{ 28.682 \cdot 0.100 } \\&= 0.346 \\[10pt] \end{aligned} \end{split}\]

Notamos que nos perjudica hacer este cambio, ya que la eficiencia disminuye.