IIQ2013 - Clase 21

import handcalcs.render
import forallpeople
import numpy as np
import forallpeople as si
from CoolProp.CoolProp import PropsSI

si.environment('default', top_level=True)

Pregunta 1

Considerando la curva típica de ebullición para agua a \(1~\text{atm}\) que se adjunta, si \(h > 104~\text{W/m}^2\cdot\text{K}\), el régimen de ebullición probablemente sea el siguiente:

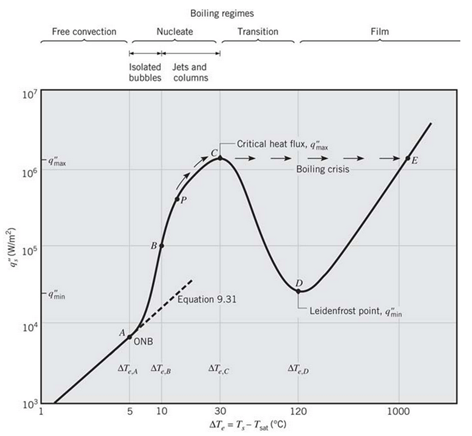
Fig. 20 Regímenes de ebullición.

(a) Ebullición de convección libre
(b) Ebullición nucleada
(c) Ebullición de transición
(d) Ebullición de película

Solución

Dado que no tenemos un valor exacto de \(h\) para el agua, procedemos a testear el límite superior de la ebullición de convección libre.

Del gráfico, asumiremos \(q = 1.6 \times 10^4~\text{W/m}^2\). Esto correspodne a una diferencia de temperatura aproximadamente de 5°C. Luego,

%%render
dT = 5
p = 1 # atm
h = 1043 * dT**(1/3) * p **(0.4) #W/m$^2\cdot$K

\[\begin{split} \begin{aligned} \mathrm{dT} &= 5 \; \\[10pt] p &= 1 \; \;\textrm{(atm)} \\[10pt] h &= 1043 \cdot \left( \mathrm{dT} \right) ^{ \left( \frac{ 1 }{ 3 } \right) } \cdot \left( p \right) ^{ 0.4 } = 1043 \cdot \left( 5 \right) ^{ \left( \frac{ 1 }{ 3 } \right) } \cdot \left( 1 \right) ^{ 0.4 } &= 1783.505 \; \;\textrm{(W/m$^2\cdot$K)} \end{aligned} \end{split}\]

Este coeficiente de convección es muy bajo, por lo tanto descartamos nucleación por convección natural. Ahora procedemos a testear el segundo límite de flux entre ebullición nucleada y ebullición de transición.

Del gráfico, asumiremos \(q = 2.4 \times 10^5~\text{W/m}^2\). Esto corresponde a una diferencia de temperatura aproximadamente de 15°C. Luego,

%%render
dT = 15
p = 1 # atm
h = 5.56 * dT**(3) * p **(0.4) #W/m$^2\cdot$K

\[\begin{split} \begin{aligned} \mathrm{dT} &= 15 \; \\[10pt] p &= 1 \; \;\textrm{(atm)} \\[10pt] h &= 5.56 \cdot \left( \mathrm{dT} \right) ^{ 3 } \cdot \left( p \right) ^{ 0.4 } = 5.56 \cdot \left( 15 \right) ^{ 3 } \cdot \left( 1 \right) ^{ 0.4 } &= 18765.000 \; \;\textrm{(W/m$^2\cdot$K)} \end{aligned} \end{split}\]

Que es mayor a \(10^4\). Este valor está en un punto medio en la región de ebullición nucleada, por lo tanto el régimen de ebullición es probablemente ebullición nucleada. Esto corresponde a la alternativa b).

Pregunta 2

Se puede afirmar lo siguiente sobre procesos de ebullición de alberca:

(a) Un número de Jakob pequeño (\(Ja < 1\)) sugiere que el calor absorbido durante el cambio de fase supera al calor sensible absorbido por la fase líquida, con el resultado de aumentar el flujo de calor.
(b) El calor máximo que se puede transferir en procesos de ebullición nucleada disminuye constantemente a medida que la presión se acerca a la presión crítica del fluido, cuando dicho calor se reduce a nada.
(c) Ambas (a) y (b) son verdaderas.
(d) Ambas (a) y (b) son falsas.

Solución

a) El número de Jakob viene dado por

\[ Ja = \frac{c_p \Delta T}{\lambda_{lv}}\]

Si el número de Jakob es pequeño, el calor sensible es muy pequeño en comparación al calor latente. Por lo tanto el calor absorbido durante el cambio de fase es mas grande que el calor absorbido por la fase líquida. Sin embargo, esto produce un menor flujo de calor. Por lo tanto, a) es incorrecta.

b) Cerca del punto crítico, el flux crítico de calor se acerca a cero, por lo tanto b) es correcta.

Pregunta 3

Considere un tubo vertical de \(50~\text{mm}\) de diámetro interior por el cual fluye agua a \(4~\text{bar}\). Si la ebullición comienza en una posición en que la pared del tubo se encuentra \(15~\text{°C}\) por sobre la temperatura de saturación, la tasa de transferencia de calor por unidad de largo de la tubería (\(q’\)) es aproximadamente la siguiente

(a) \(q’\) \(>\) \(1000\) \(\text{kW/m}\)
(b) \(500\) \(<\) \(q’\) \(\leq\) \(1000\) \(\text{kW/m}\)
(c) \(100\) \(<\) \(q’\) \(\leq\) \(500\) \(\text{kW/m}\)
(d) \(q’\) \(\leq\) \(100\) \(\text{kW/m}\)

Solución

Primero calculamos el coeficiente de convección para ebullición nucleada en una superficie vertical. En primer lugar iteramos el primer tramo de la ecuación:

%%render
dT = 15 # C
p = 4 # bar
h = 537 * dT**(1/7) * p **0.4
q = h*dT

\[\begin{split} \begin{aligned} \mathrm{dT} &= 15 \; \;\textrm{(C)} \\[10pt] p &= 4 \; \;\textrm{(bar)} \\[10pt] h &= 537 \cdot \left( \mathrm{dT} \right) ^{ \left( \frac{ 1 }{ 7 } \right) } \cdot \left( p \right) ^{ 0.4 } = 537 \cdot \left( 15 \right) ^{ \left( \frac{ 1 }{ 7 } \right) } \cdot \left( 4 \right) ^{ 0.4 } &= 1376.611 \\[10pt] q &= h \cdot \mathrm{dT} = 1376.611 \cdot 15 &= 20649.169 \end{aligned} \end{split}\]

Sin embargo, esto muestra que estamos fuera del rango de validez del coeficiente de convección para flujo bajo, ya que \(q = 20,6 kW m^{-2} > 3 kW m^{-2}\). Repetimos el cálculo con la otra ecuación.

%%render
dT = 15 # C
p = 4 # bar
h = 7.95 * dT**(3) * p **0.4
q = h*dT

\[\begin{split} \begin{aligned} \mathrm{dT} &= 15 \; \;\textrm{(C)} \\[10pt] p &= 4 \; \;\textrm{(bar)} \\[10pt] h &= 7.95 \cdot \left( \mathrm{dT} \right) ^{ 3 } \cdot \left( p \right) ^{ 0.4 } = 7.95 \cdot \left( 15 \right) ^{ 3 } \cdot \left( 4 \right) ^{ 0.4 } &= 46715.920 \\[10pt] q &= h \cdot \mathrm{dT} = 46715.920 \cdot 15 &= 700738.794 \end{aligned} \end{split}\]

Con lo que concluimos que \(q = 700 kW m^{-2}\), por ende la alternativa b) es la correcta.