Ejercicio 1: Momentum y Fuerza

Enunciado

La ecuación de Bernoulli proviene de un equilibrio entre la fuerza que ejerce la variación de presión, el peso del fluido y la variación de Momentum a lo largo de la tubería (Si se ignora el efecto de la fricción en la superficie de la tubería). Para entender mejor la relación de Momentum y fuerza, su profesor le propone el siguiente caso:

Un flujo de agua a 25°C con densidad \(\rho = 997.05 \hspace{1mm}(kg/m^3)\) baja a velocidad constante por un sistema de tuberías cilíndricas hasta alcanzar un codo, cambiando su trayectoria. Este codo se encuentra sujetado por un fierro metálico. Si la velocidad del flujo es \(u = 3 \hspace{1mm}(m/s)\), ¿A qué fuerza se somete el codo considerando únicamente el efecto de la variación de Momentum producido por el flujo?

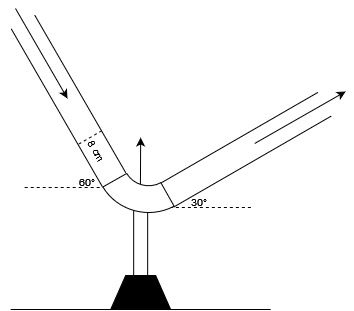
Fig. 1 Tubería y codo

Información sobre la figura

El diámetro de la tubería es constante y de 8 cm, la tubería que baja se encuentra inclinada 60° respecto al eje X y la que sube se encuentra a 30°

Ver solución

Solución

#Paquetes utilizados
import handcalcs.render
from handcalcs import handcalc
from math import pi, sin, cos, radians

Del enunciado obtenemos los siguientes datos

%%render long
rho = 997.05 #kg/m3
u = 3 #m/s
d = 0.08 #m

\[\begin{split} \begin{aligned} \rho &= 997.050 \; \;\textrm{(kg/m3)} \\[10pt] u &= 3 \; \;\textrm{(m/s)} \\[10pt] d &= 0.080 \; \;\textrm{(m)} \end{aligned} \end{split}\]

El área transversal por el cual pasa el flujo es

%%render long
A = pi*(d/2)**2 #m2

\[\begin{split} \begin{aligned} A &= \pi \cdot \left( \frac{ d }{ 2 } \right) ^{ 2 } \\&= 3.142 \cdot \left( \frac{ 0.080 }{ 2 } \right) ^{ 2 } \\&= 0.005 \; \;\textrm{(m2)}\\[10pt] \end{aligned} \end{split}\]

Luego la variación de Momentum vendrá dada por

%%render long
M = rho*u**2*A #N

\[\begin{split} \begin{aligned} M &= \rho \cdot \left( u \right) ^{ 2 } \cdot A \\&= 997.050 \cdot \left( 3 \right) ^{ 2 } \cdot 0.005 \\&= 45.105 \; \;\textrm{(N)}\\[10pt] \end{aligned} \end{split}\]

Ya que la tubería se encuentra inclinada, debemos descomponer el vector de fuerzas en su eje X e Y. Para la sección de la tubería que baja la fuerza que ejerce va en la dirección de aceleración del fluido.

%%render long
M_Ybaja = -M*sin(pi/3) #N
M_Xbaja = M*cos(pi/3) #N

\[\begin{split} \begin{aligned} M_{Ybaja} &= \left( - M \right) \cdot \sin \left( \frac{ \pi }{ 3 } \right) \\&= \left( - 45.105 \right) \cdot \sin \left( \frac{ 3.142 }{ 3 } \right) \\&= -39.062 \; \;\textrm{(N)}\\[10pt] \\[10pt] M_{Xbaja} &= M \cdot \cos \left( \frac{ \pi }{ 3 } \right) \\&= 45.105 \cdot \cos \left( \frac{ 3.142 }{ 3 } \right) \\&= 22.553 \; \;\textrm{(N)}\\[10pt] \end{aligned} \end{split}\]

De manera análoga para la tubería que sube.

%%render long
M_Ysube = M*sin(pi/6) #N
M_Xsube = M*cos(pi/6) #N

\[\begin{split} \begin{aligned} M_{Ysube} &= M \cdot \sin \left( \frac{ \pi }{ 6 } \right) \\&= 45.105 \cdot \sin \left( \frac{ 3.142 }{ 6 } \right) \\&= 22.553 \; \;\textrm{(N)}\\[10pt] \\[10pt] M_{Xsube} &= M \cdot \cos \left( \frac{ \pi }{ 6 } \right) \\&= 45.105 \cdot \cos \left( \frac{ 3.142 }{ 6 } \right) \\&= 39.062 \; \;\textrm{(N)}\\[10pt] \end{aligned} \end{split}\]

Finalmente, la fuerza total que ejerce el fluido sobre el codo es,

%%render long
F_Y = M_Ybaja + M_Ysube #N
F_X = M_Xbaja + M_Xsube #N

\[\begin{split} \begin{aligned} F_{Y} &= M_{Ybaja} + M_{Ysube} \\&= -39.062 + 22.553 \\&= -16.510 \; \;\textrm{(N)}\\[10pt] \\[10pt] F_{X} &= M_{Xbaja} + M_{Xsube} \\&= 22.553 + 39.062 \\&= 61.615 \; \;\textrm{(N)}\\[10pt] \end{aligned} \end{split}\]