Ejercicio 1: Estanques agitados

Enunciado

Lo contrataron en una empresa de apicultores como ingeniero químico encargado de procesos. Su primer trabajo, será estudiar el comportamiento de la miel en un estanque agitado. Los investigadores hicieron un análisis reológico de la miel que se produce, y obtuvieron experimentalmente que la densidad de esta miel es de \(\rho = 1360\hspace{1mm}(kg/m^3)\) y su viscocidad es de \(\mu = 5647\hspace{1mm}(cP)\). La empresa cuenta con un estanque con configuración estándar (\(S_6 = 1\)), cuya altura es de \(H = 2.5\hspace{1mm}(m)\), considere que el estanque se llena a su máxima capacidad. Por útlimo, la empresa cuenta un un motor para el agitador con consumo de potencia de hasta 35 kW. Responda lo siguiente:

1. Elija el agitador que la empresa debería comprar para la miel. Discuta la opción de agregar deflectores.

2. La única configuración geométrica con la que cuenta el proveedor de agitadores es axial. En específico, este tiene disponible agitadores tipo A-2. Determine si el motor es adecuado para operar a \(300 RPM\). Asuma que \(S_1 = 1/3\).

3. Encuentre la velocidad de agitación máxima a la que puede operar este motor en las condiciones descritas. Asuma que la potencia es independiente del número de Reynolds. Compuebe si este supuesto es válido una vez obtenga el resultado.

4. Utilizando la velocidad de agitación máxima, obtenga el tiempo de mezclado considerando que se agregaron deflectores.

Ver solución

Solución

# Paquetes utilizados
import handcalcs.render
from handcalcs import handcalc
from math import pi

Inciso 1

Para saber qué agitador utilizar, debemos saber el volumen del estanque y la viscosidad del fluido.

%%render long
S_6 = 1
H = 2.5 #m
D_t = H/S_6 #m
V_t = pi*(D_t/2)**2*H #m$^3$

\[\begin{split} \begin{aligned} S_{6} &= 1 \; \\[10pt] H &= 2.500 \; \;\textrm{(m)} \\[10pt] D_{t} &= \frac{ H }{ S_{6} } \\&= \frac{ 2.500 }{ 1 } \\&= 2.500 \; \;\textrm{(m)}\\[10pt] \\[10pt] V_{t} &= \pi \cdot \left( \frac{ D_{t} }{ 2 } \right) ^{ 2 } \cdot H \\&= 3.142 \cdot \left( \frac{ 2.500 }{ 2 } \right) ^{ 2 } \cdot 2.500 \\&= 12.272 \; \;\textrm{(m$^3$)}\\[10pt] \end{aligned} \end{split}\]

A continuación nos ubicamos en el gráfico.

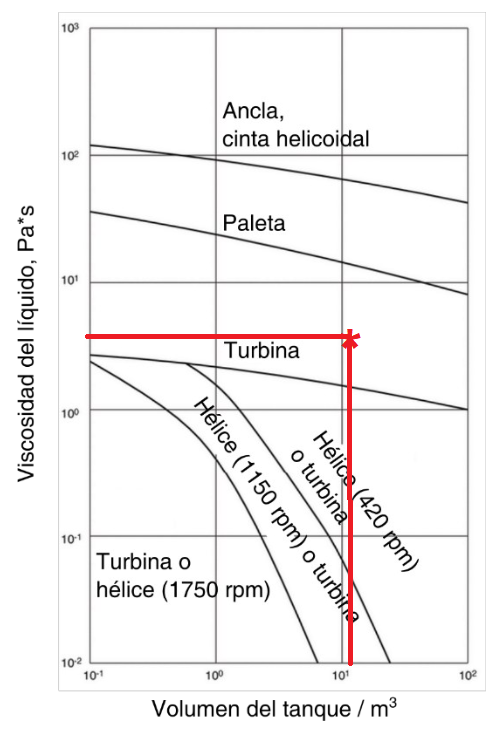
Fig. 6 Selección de agitador.

Observamos que nos encontramos aproximadamente en un área donde es recomendable utilizar turbinas.

En cuanto a la utilización de deflectores, esta sí es combeniente ya que los agitadores de turbina no pasan cerca de la pared del estanque.

Inciso 2

Para saber si el motor disponible es adecuado, debemos saber el consumo de potencia teórico que este tendría si opera a las condiciones descritas. Ya que tenemos el modelo, podemos utilizar el gráfico para recuperar el número de potencia. Calculamos el número de Reynolds

%%render long
mu = 5.647 #Pa$\cdot$s
rho = 1360 #kg/m$^3$
N = 300/60 #RPS
S_1 = 1/3
D_a = S_1*D_t #m
Re = (rho*N*D_a**2)/mu

\[\begin{split} \begin{aligned} \mu &= 5.647 \; \;\textrm{(Pa$\cdot$s)} \\[10pt] \rho &= 1360 \; \;\textrm{(kg/m$^3$)} \\[10pt] N &= \frac{ 300 }{ 60 } &= 5.000 \; \;\textrm{(RPS)} \\[10pt] S_{1} &= \frac{ 1 }{ 3 } &= 0.333 \\[10pt] D_{a} &= S_{1} \cdot D_{t} \\&= 0.333 \cdot 2.500 \\&= 0.833 \; \;\textrm{(m)}\\[10pt] \\[10pt] \mathrm{Re} &= \frac{ \rho \cdot N \cdot \left( D_{a} \right) ^{ 2 } }{ \mu } \\&= \frac{ 1360 \cdot 5.000 \cdot \left( 0.833 \right) ^{ 2 } }{ 5.647 } \\&= 836.236 \\[10pt] \end{aligned} \end{split}\]

Obtenemos el número de potencia utilizando el gráfico.

A continuación nos ubicamos en el gráfico.

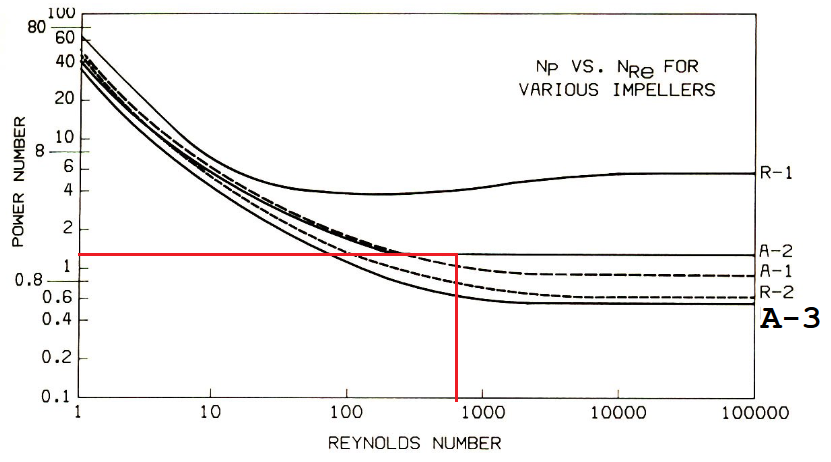
Fig. 7 Número de potencia en función del número de Reynolds.

Notamos que para este valor de Reynolds y para el agitador seleccionado, el valor de \(K\) se encuentra en la zona de independencia de Reynolds, en donde \(K=K_T\approx 1.3\). Sabemos que para esta sección, el consume de potencia es:

\[ P = K_T\rho N^3D_a^5 \]

%%render long
K_T = 1.3
P = K_T*rho*N**3*D_a**5 #W

\[\begin{split} \begin{aligned} K_{T} &= 1.300 \; \\[10pt] P &= K_{T} \cdot \rho \cdot \left( N \right) ^{ 3 } \cdot \left( D_{a} \right) ^{ 5 } \\&= 1.300 \cdot 1360 \cdot \left( 5.000 \right) ^{ 3 } \cdot \left( 0.833 \right) ^{ 5 } \\&= 88814.943 \; \;\textrm{(W)}\\[10pt] \end{aligned} \end{split}\]

Podemos observar que \(35\hspace{1mm}kW<88.8\hspace{1mm}kW\). Por la tanto el motor no esta apto para trabajar en dichas condiciones.

Inciso 3

Nos dicen que asumamos que el número de potencia es independiente del número de Reynolds. Luego \(n=0\) en:

\[ Np = K\cdot Re^n \]

A partir de esto trabajamos en el supuesto de que \(K\) es constante e igual a \(K_T\). Entonces podemos despejar \(N\).

\[ N = \sqrt[3]{\frac{P}{K_T\rho D_a^5}} \]

%%render long
P_max = 35000 #W
N_max = (P_max/(K_T*rho*D_a**5))**(1/3) #RPS

\[\begin{split} \begin{aligned} P_{max} &= 35000 \; \;\textrm{(W)} \\[10pt] N_{max} &= \left( \frac{ P_{max} }{ K_{T} \cdot \rho \cdot \left( D_{a} \right) ^{ 5 } } \right) ^{ \left( \frac{ 1 }{ 3 } \right) } \\&= \left( \frac{ 35000 }{ 1.300 \cdot 1360 \cdot \left( 0.833 \right) ^{ 5 } } \right) ^{ \left( \frac{ 1 }{ 3 } \right) } \\&= 3.666 \; \;\textrm{(RPS)}\\[10pt] \end{aligned} \end{split}\]

print(f"La velocidad máxima de agitación es de {N_max*60:g} RPM")

La velocidad máxima de agitación es de 219.946 RPM

Comprobamos si nuestro supuesto para \(K_T\) es correcto mediante el número de Reynolds.

%%render long
Re = (rho*N_max*D_a**2)/mu

\[\begin{split} \begin{aligned} \mathrm{Re} &= \frac{ \rho \cdot N_{max} \cdot \left( D_{a} \right) ^{ 2 } }{ \mu } \\&= \frac{ 1360 \cdot 3.666 \cdot \left( 0.833 \right) ^{ 2 } }{ 5.647 } \\&= 613.088 \\[10pt] \end{aligned} \end{split}\]

A partir del gráfico comprobamos que, para un agitador con geometría A-2, el supuesto es válido para el cambio de las revoluciones por minuto.

Inciso 4

Tenemos el siguiente gráfico que relciona el factor de tiempo de mezclado \((N\times t_M)\) con el número de Reynolds.

A continuación nos ubicamos en el gráfico.

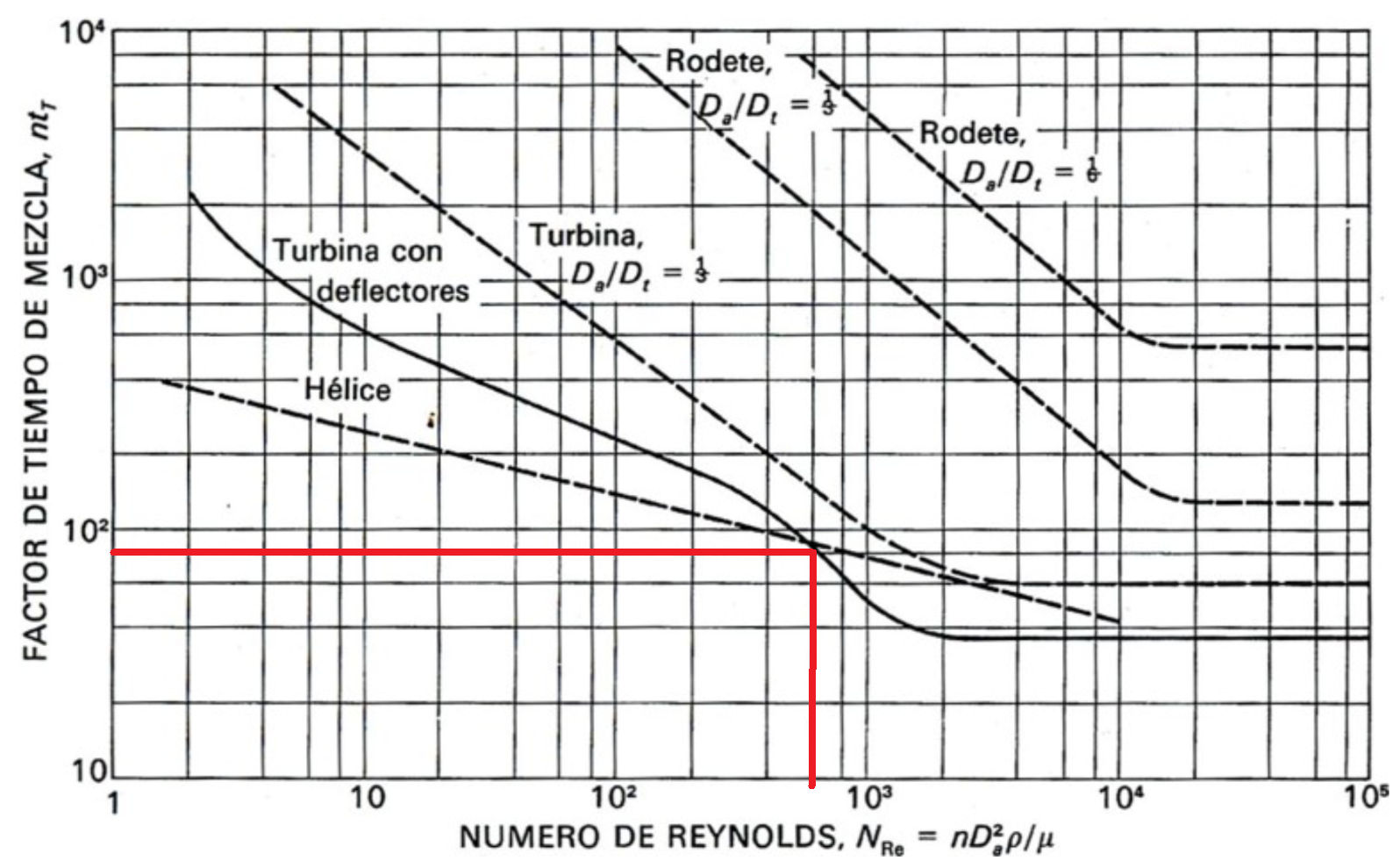
Fig. 8 Relación entre el factor de timpo de mezcla y el número de Reynolds.

Obtenemos que \(N\times t_M \approx 80\). Luego calculamos el tiempo de mezclado.

%%render long
t_m = 80/N_max #s

\[\begin{split} \begin{aligned} t_{m} &= \frac{ 80 }{ N_{max} } \\&= \frac{ 80 }{ 3.666 } \\&= 21.824 \; \;\textrm{(s)}\\[10pt] \end{aligned} \end{split}\]

El tiempo de mezclado será de 21.8 segundos.