Ejercicio 3: Bombas y eficiencia#
Enunciado#
Entra benceno a \(37.8~\text{°C}\) el cual debe ser bombeado a caudal \(11~\text{m}^3\text{/h}\). El modelo de la bomba es tipo \(3656/3756~\text{Grupo-S}\), con un rodete \(\text{B}\) de diámetro \(7.75~\text{in}\). El benceno se transporta desde un estanque hasta otro tal y como muestra la figura. Ambos estanques se encuentran a \(3~\text{atm}\). La altura entre los puntos \(\text{a'}\) y \(\text{a}\) es \(10~\text{m}\) y la altura entre los puntos \(\text{b}\) y \(\text{b'}\) es de \(2~\text{m}\). Las tuberías tienen un diámetro de \(12~\text{cm}\). La densidad del benceno a la temperatura de operación es de \(865~\text{kg/m}^3\) y su presión de vapor es \(26.2~\text{kPa}\). Si la altura asociada a las perdidas por fricción es \(h_f = 3~\text{m}\) y los codos son codos cuadrados.\
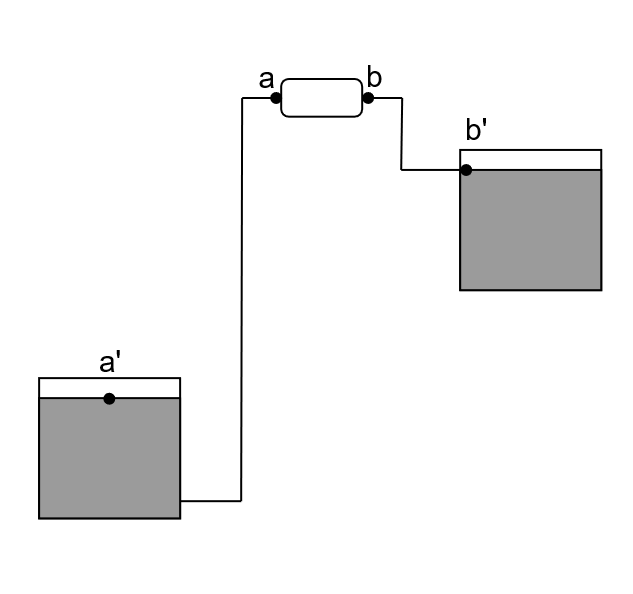
Fig. 4 Sistema de tuberías, bombas y estanques.#
Responda lo siguiente:
Demuestre la ecuación que describe el trabajo de la bomba (\(\eta W_p\)) a partir de las ecuaciones de bernoulli para los puntos \(\text{a'-a}\), \(\text{a-b}\) y \(\text{b-b'}\).
Encuentre la altura de la bomba (\(h_B\)) en \(\text{m}\).
Calcule la potencia requerida por la bomba (\(P_m\)) en \(\text{W}\).
Determine si la bomba cavita considerando que la altura asociada a las perdidas por fricción entre \(\text{a'}\) y \(\text{a}\) contribuyen \(2/3\) de las pérdidas totales por fricción.
Solución#
import handcalcs.render
handcalcs.set_option("custom_symbols",{"ap": "a'", "bp": "b'", "eta": "\eta ", "dotm": "\dot m"})
from numpy import pi
Inciso 1#
Para el primer tramo (\(\text{a'-a}\)), la ecuación de bernoulli será:
Para el tramo \(\text{a-b}\):
Por último, para el tramo \(\text{b-b'}\):
Despejando en la ecuación de bernoulli entre los puntos \(\text{a-b}\).
Luego, podemos entender la suma de las pérdidas de carga por fricción y singularidades entre \(\text{a'-a}\) y \(\text{b-b'}\) como las pérdidas de cargas en todo el sistema.
Finalmente llegamos a la última ecuación:
Para que la ecuación sea consistente con la figura, consideremos que \(Z_{a'}=0\) y que ambos estanques se encuentran a la misma presión (\(3~\text{atm}\)), la cual será la referencia \(P_{a'}=P_{b'}=0\). Además, el punto \(\text{a'}\) se considera sin movimiento (\(V_{a'}=0\)) por el supuesto de estanque muy grande. Reordenando:
Luego, reemplazando las pérdidas de carga y asumiendo que la velocidad el todo el sistema (excluyendo el estanque) es constante:
Inciso 2#
Ya que en el enunciado nos entregan las pérdidas de carga por fricción en \(\text{m}\), escribmos la función para \(\eta W_p\) de la siguiente manera:
%%render params
g = 9.81 #m/s$^2$
Z_bp = 10-2 #m
D = 12/100 #m
K_codo = 1.2
K_salida = 0.5
K_entrada = 1.0
Q = 11/3600 #m$^3$/s
h_f = 3 #m
rho = 865 #kg/m$^3$
%%render long
etaW_p = g*Z_bp + (1 + (K_salida + 4*K_codo + K_entrada))*(8*Q**2)/(pi**2*D**4) + g*h_f #J/kg
%%render long
h_B = etaW_p/g #m
Inciso 3#
Del gráfico para la bomba tipo \(3656/3756~\text{Grupo-S}\) con rodete \(\text{B}\) de diámetro \(7.75~\text{in}\), vemos que para un caudal de \(11~\text{m}^3\text{/h}\) la eficiencia es aproximadamente de un \(\eta = 65~\%\).
La fórmula para la potencia requerida puede ser escrita como:
%%render long
eta = 0.65
dotm = Q*rho #kg/s
P_B = dotm*etaW_p/eta #W
Inciso 4#
Debemos compara \(\text{NPSH}_d\) con \(\text{NPSH}_r\). Del gráfico, \(\text{NPSH}_r \approx 17.5~\text{m}\).
Para la \(\text{NPSH}_d\) sabemos que:
%%render params
P_v = 26.2*1000 #Pa
P_ap = 3*101325 #Pa
z_a = 10 #m
h_f = 2 #m
%%render long
NPSH_d = (P_ap-P_v)/(rho*g) - z_a - (1+(K_salida+4*K_codo+K_entrada))*(8*Q**2)/(g*pi**2*D**4) - h_f #m
Ya que \(\text{NPSH}_d>\text{NPSH}_r\), la bomba no cavita.
